Research

These are the projects based on my academic research career, i.e. my Ph.D. and my current PostDoc.

MeLODy | Sept 2021 - Now

Investingating how we can using machine learning in observation and computational oceanography. Specifically, we are working with geophysical observations obtained from satellite altimetry and we would like to constrain the solution with ocean models, e.g. NEMO, MITGCM. We approach this problem from a data assimilation formulation but with a machine learning perspective. Currently, we have broken this problem into 3 parts:

  1. Using Neural Fields to interpolate sparse, noisy sea surface height data from altimetry satellites (nerf4ssh)
  2. Using conditional generative models to learn surrogate models (cflow4surrgate)
  3. Using neural networks to solve 4DVar problems (modern4dvar)

For more information, see the following resources:

ERC | Mar 2017 - Sep 2020

(a) SAKAME

(b) EGP

Figure 1: Summary figures of my work under the ERC project.

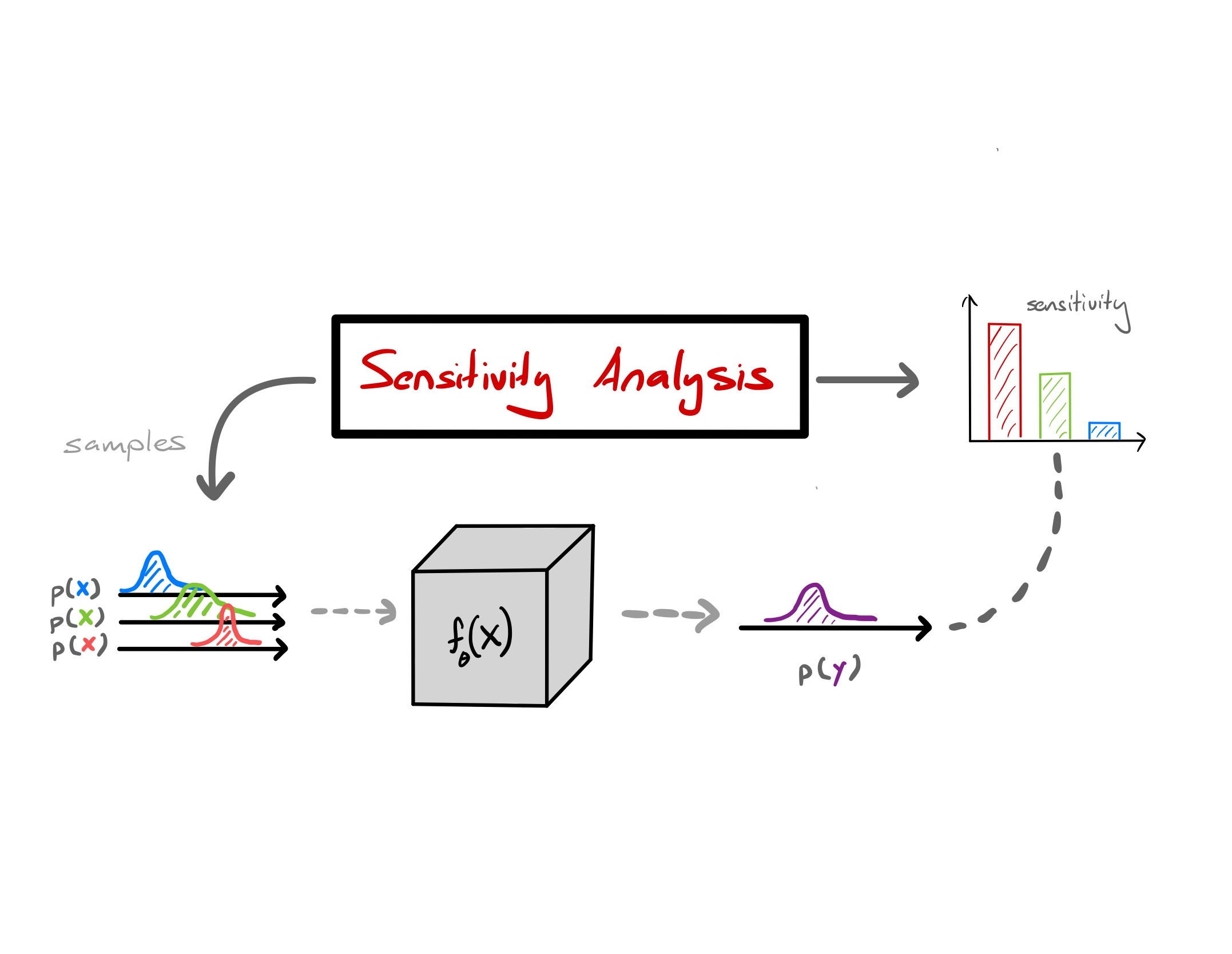
In this project, I looked at various ways we could use machine learning to characterize uncertainty in geoscience applications. ML is useful but it is often not understood. However, we demonstrate that there are two aspects that would help alleviate the idea that ML is a “black-box”: 1) error propagation and 2) sensitivity analysis.

TLDR: Investigating some connections between derivatives of kernel methods and standard sensitivity analysis in the physical sciences.

We looked at how there is a connection between the derivatives of kernel methods and standard sensitivity analysis seen in the physical sciences. We looked at

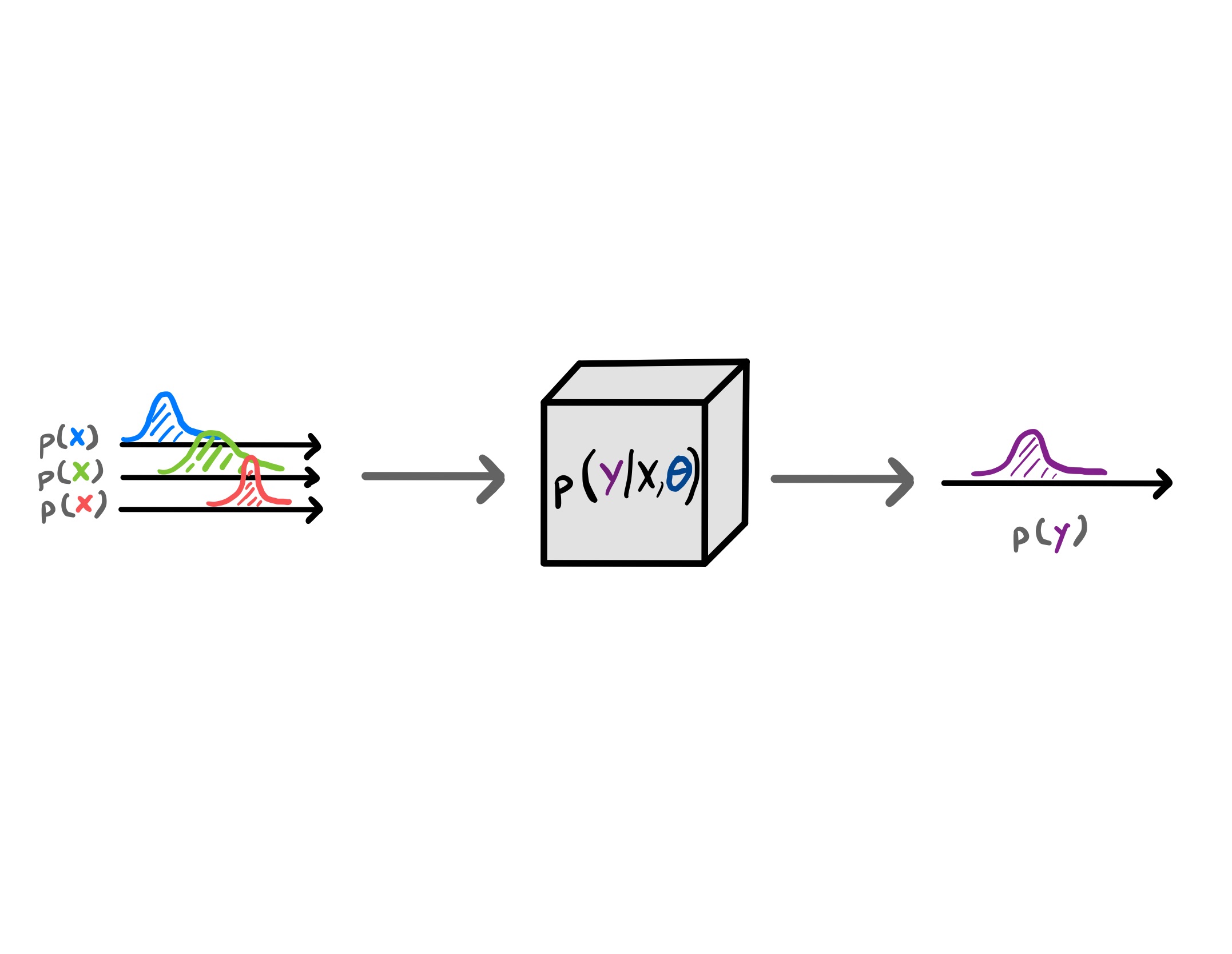
TLDR: Investigating how we can do error propagation through Gaussian process regression model.

In this project I looked at how we can propagate input uncertainty through GP regression models. GPs are the gold standard for having well calibrated predictive mean and variances. However, there is not much (recent) research on how we can propagate input uncertainty. So we looked at how this was possible in the context of geoscience.

  • Journal Article: Showcasing how derivatives of kernel methods are linked to
  • GitHub Repo: all experiments are in here.
  • Research Journal: A detailed walkthrough on the literature for input uncertainty in Gaussian processes.

USMILE | Sept 2020 - Aug 2021

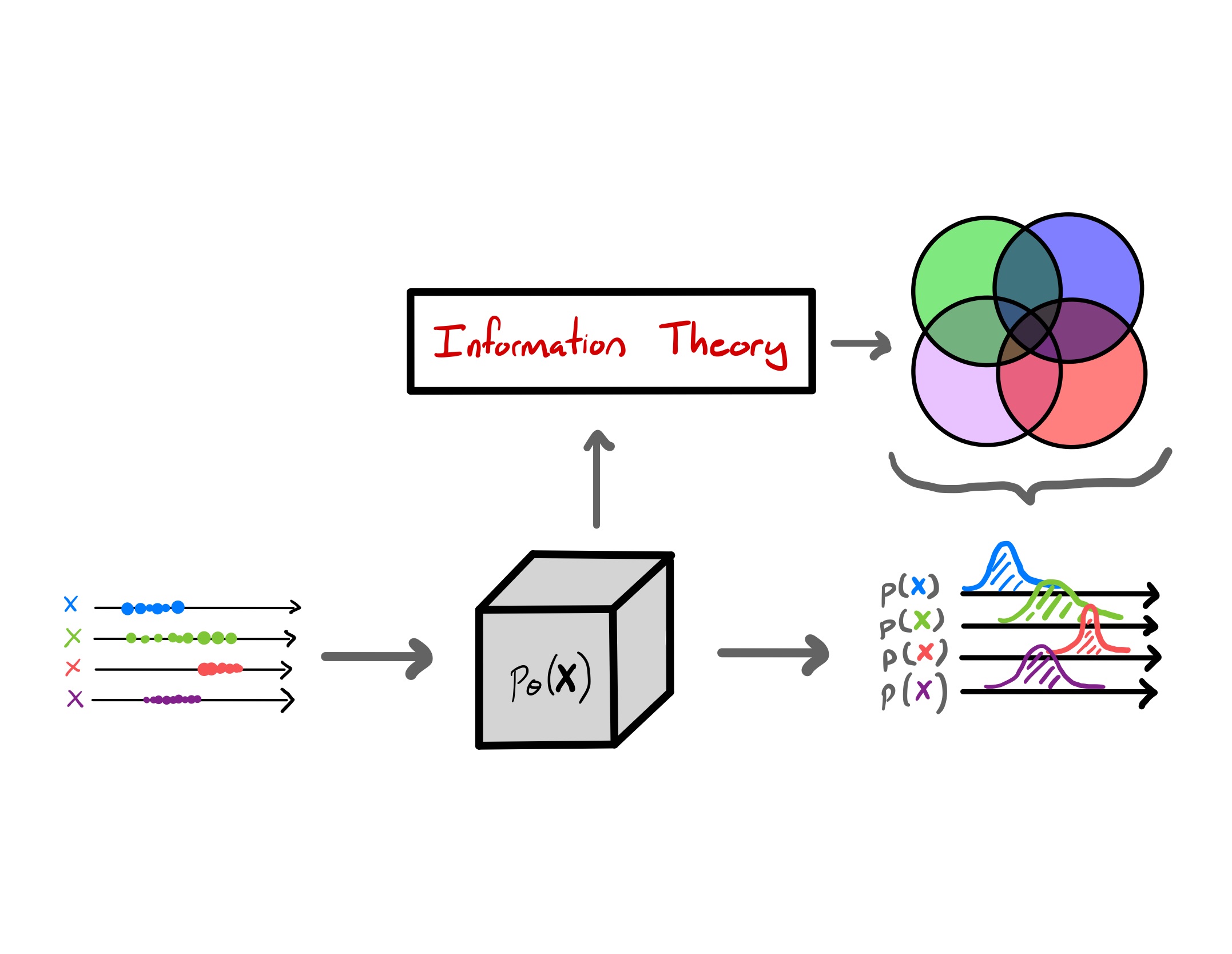
Figure 2: Summary figures of my work under the USMILE project.

In this project, I looked at how we could use different machine learning methods to extract information from Earth System Data. We were given a massive amount of reanalysis data from various sources and we were interested to see how ML can be useful to extract information from said cubes. However, information theory is a difficult problem due to the curse of dimensionality which prohibits good density estimators that are necessary for said information theoretic metrics. We look at Gaussianization as a good density estimator with direct links to information theory due to the formulation.

TLDR: We give a empirical deep-dive into showing how Gaussianization is a good information theoretic estimator.

Gaussianization is a long standing density estimation method. In fact it is the first ever “normalizing flow” method within the literature. We look at a particular version which is called the Rotation-Based Iterative Gaussianization method. We demonstrate its usefulness in including 1) time-memory for drought indicators, 2) redundancy in hyperspectral images, 3) sampling for hyperspectral images, and 4) entropy for different spatial-temporal configurations.

More resources for this project:

  • Journal Article - Published work on formulation and applications to EO data.
  • GitHub Repo - All codes for experiments with Gaussianization and Earth observation data.
  • rbig - A numpy python package that implements the iterative Gaussianization method.
  • rbig_jax - A JAX python package that implements the iterative and parametric Gaussianization method.
  • Awesome-Normalizing-Flows - An indepth literature review of normalizing flows (and Gaussianization)

TLDR: We showcase how Gaussianization is a good density estimator and information theoretic estimator for various in Geoscience applications.

In this project, we take a deep-dive into the Gaussianization formulation and demonstrate empirically how it can be used to estimate information theoretic quantities like entropy, mutual information, multivariate mutual information and the Kullback-Leibler Divergence.

  • Submitted Article - Work for the formulation and empirical evidence for its usefulness in different applications.
  • Project Webpage - official webpage for the project and article
  • GitHub Repo - All codes for experiments with Gaussianization and Earth observation data.
  • rbig_matlab - A matlab package that implements the iterative Gaussianization method and corresponding IT methods.
  • rbig_jax - A JAX python package that implements the iterative and parametric Gaussianization method.

Machine Learning “Sprints”

This are the projects that I was a part of for sprints; where I was a part of a multidisciplinary team looking to solve an applied problem using machine learning.

FDL Sprint (GLM) | Jun 2021 - Aug 2021

Figure 3: Summary figures of the FDL Sprint project [Slides].

In this project, we were concerned with extracting lightning events from the GLM Lightning mapper. I was a part of a team that built an end-to-end machine learning pipeline that was able help do filter the point clouds and extract features that were indicative of lightning. We tried the standard techniques like PCA, some deep learning techniques like AutoEncoders, and finally some new SOTA like Graphical Neural Networks.

For more resources see:

ML4CC Sprint | Jan 2021 - Mar 2021

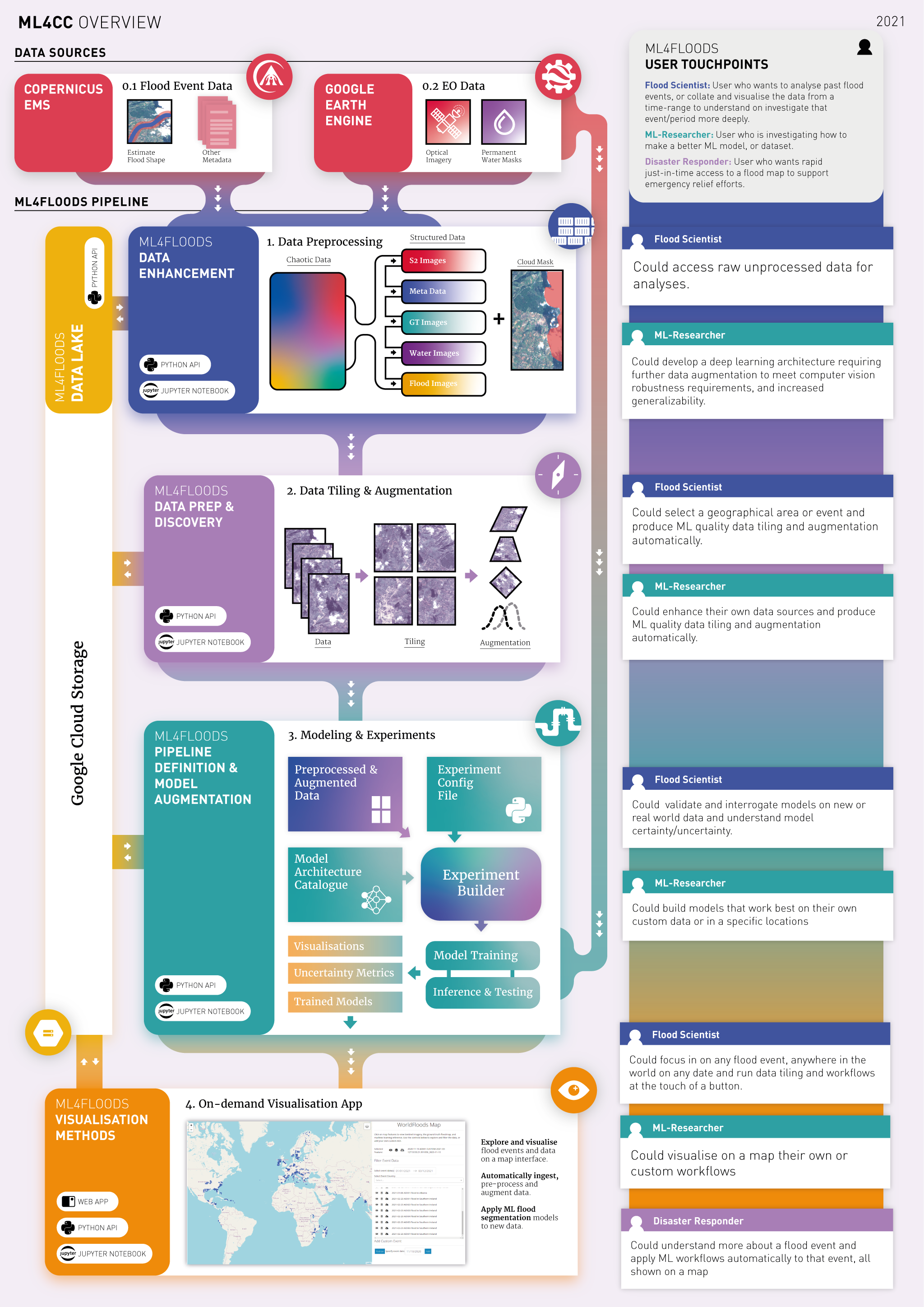
Figure 4: Summary figures of the ML4CC project [Source].

In this project, we were concerned with predicting flood extent after a large storm via an onboard model on a satellite. I was a part of a team that built an end-to-end machine learning pipeline that was able help do just that. We implemented the following pipeline:

  1. downloads multimodel remotely sensed multispectral images
  2. preprocesses heterogeneous data accordingly
  3. augments the images to increase sample size for training
  4. train a neural network model for image segmentation
  5. download a trained model to perform inference
  6. visualize the image segmented image

For more resources see:

FDL Sprint (StarSpots) | Jun 2020 - Aug 2020

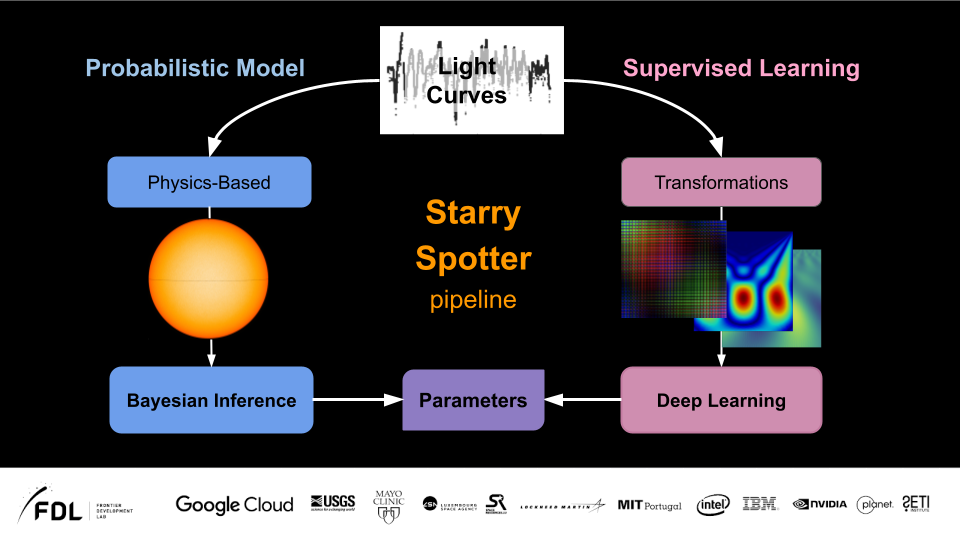
Figure 5: Summary figures of the FDL Spring project [Slides].

In this project, we were concerned with predicting spots on stars (as an indicator of star activity) from telescope data. I was a part of a team that built an end-to-end machine learning pipeline that was able help do just that. We were able to fit the data to get parameters using Bayesian inference. We were also able to use a neural network to predict star spot properties using transfer learning resulting in a x10K speed up!

For more resources see: